[딥러닝] 04. 선형회귀

1. 선형회귀

• 회귀 : 일반적으로 데이터들을 2차원 공간에 찍은 후, 그 데이터들을 가장 잘 설명하는 직선이나 곡선을 찾는 문제
  • => 선형 모델을 사용해 회귀 문제를 풀면 선형회귀(linear regression)라고 함.
    • ex) 부모의 키와 자녀 키의 관계 / 면적에 따른 주택 가격 / 공부시간과 학점과의 관계 등
• 선형 회귀 소개
  • 선형회귀 식은 직선의 방정식으로부터 비롯 됨...
    • 직선의 방정식) f(x) = mx + b
      • => 선형회귀는 입력 데이터를 가장 잘 설명하는 직선의 기울기(m)와 절편(b)을 찾는 문제... 머신러닝에선 기울기(m) → 가중치(weight) / 절편(b) → 바이어스(b) 라고 함.
    • 선형회귀 식) f(x) = wx + b
      • 가중치와 바이어스 값에 따라 여러 개의 직선이 있을 수 있음!
• 선형회귀의 종류
  • 단순 선형 회귀 : 독립변수(x)가 하나인 선형회귀
    
    • f(x) = wx + b
  • 다중 선형 회귀 : 독립 변수가 여러 개인 경우(입력이 여러개)
    • 이때 w1, w2, w3는 계수 또는 가중치를 나타내고, 모델이 학습하려고 하는 매개변수임.
    • x, y, z(또는 x1, x2, x3)는 각 정보의 속성을 나타냄.

또는

라고 표기함.

• 선형회귀의 원리
  • 그림1처럼 데이터에 따라 여러 직선들이 이렇게 있다면, 그림2처럼 최적의 직선을 찾는 게 선형회귀다..!
    
    • 이때, 데이터와 직선의 간격이 적을수록 좋은 직선
      • => 간격이 음수일 수도 있으니 제곱해 모두 합한 값을 손실함수(loss function) or 비용함수(cost function)이라고 함.

• 손실함수
  • n = 훈련 데이터 개수

일반 수식

argmin 표기법 - Lss()함수를 최소화 하는 w, b를 계산한다.

 

2. 선형 회귀에서 손실 함수 최소화 방법 

• 분석적인 방법 : 독립변수와 종속변수가 각각 하나인 선형회귀(최소제곱법 이용)
  • 단, 독립변수가 여러 개이면 적용 X

• 경사하강법(gradient descent method)
  • 손실함수가 어떤 형태라도, 매개(독립) 변수가 아무리 많아도 적용할 수 있는 일반적인 방법... 점진적인 학습 가능
  • 현재 위치에서의 경사(기울기)를 이용해 방향을 잡는 방법(가중치를 손실이 줄어드는 방향으로 움직임)
  • 학습률이 크면 업데이트되는 양이 커지고, 작으면 업데이트 되는 양이 작아짐... 학습률은 학습속도를 조절할 수 있다.

• 지역최소값 문제
  • 말로 설명하기 어려우니 그림으로 이해하자. (왜 일어나냐면 함수 모양을 모르기 때문에)

• 선형회귀에서 경사하강법
  • 손실(모든 데이터 포인트의 손실을 제곱해 합한 후 평균 낸 값) 함수
  • f(xi)는 모델 예측 값, yi는 실제 값

일반 수식

      (1) w, b를 모두 0으로 설정 & 학습률(한번에 기울기를 변경하는 양)을 0.01이라고 함.

      (2) 손실함수를 w에 대해아 편미분 하면

      (3) 손실함수를 b에 대해 미분하면

      (4) w와 b룰 다음과 같이 업데이트

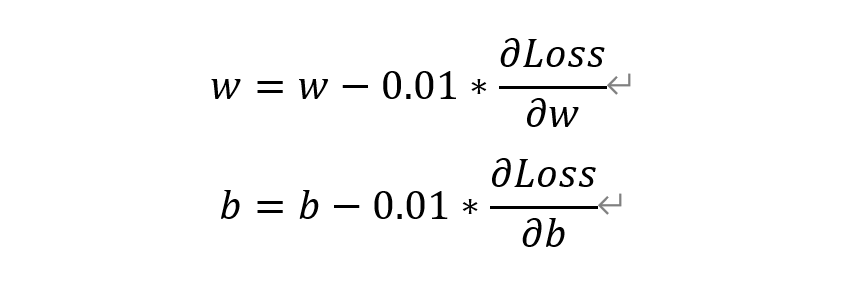
      (2)~(4)를 손실 함수 값이 아주 작아질 때까지 반복

 

3. 선형 회귀 파이썬 구현 #1 ~ 4. 선형 회귀 파이썬 구현 #2 (149~154 생략)

 

5. 과잉 적합 vs 과소 적합

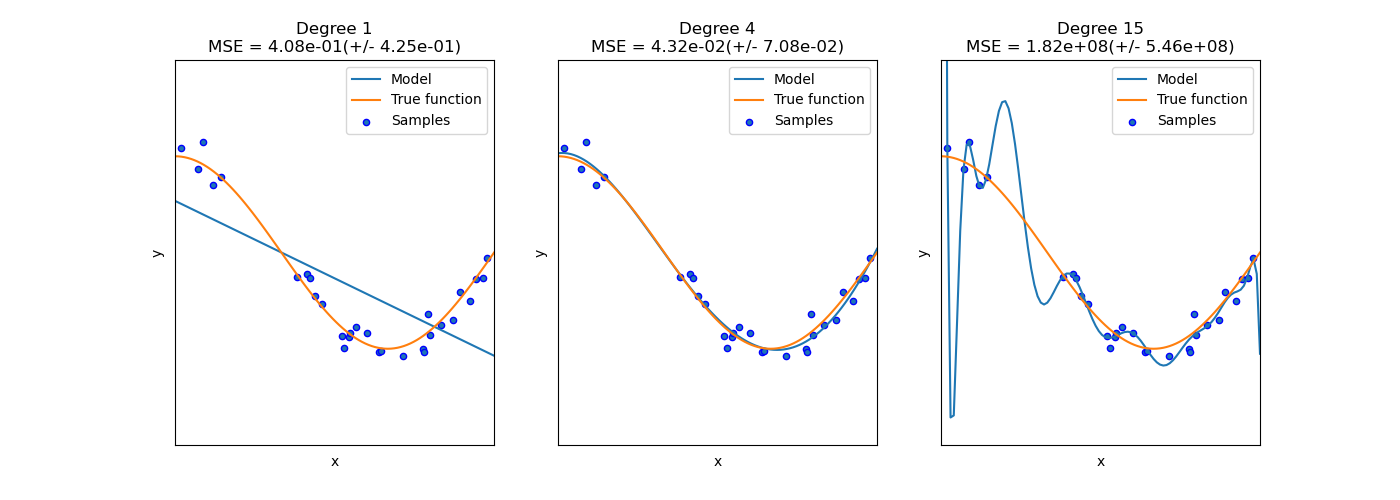
• 과잉적합(overfitting) : 훈련데이터에선 성능이 뛰어나지만, 테스트 데이터(일반화)에 대해선 성능이 잘 나오지 않는 모델을 생성하는 것
• 과소적합(underfitting) : 학습데이터와 테스트데이터 모두 성능이 좋지 않은 경우... 이 경우는 모델 자체가 적합치 않은 경우가 많아 더 나은 모델을 찾아야 함.
• (a) : 과소적합 / (b) : 적합 / (c) : 과잉적합

 

 

 

딥러닝 EXPRESS 04. 선형회귀 (p.140 ~ 159)